My Approach to Solving Wordle

#Quick Introduction

At this point many people know about Wordle. I expect anyone reading this knows about it and its rules, so I’ll keep this intro short.

Wordle is a word game where you have to guess a 5 letter word. You have 6 tries to guess it. Once you try a word, each letter is marked with a different color:

• Gray: the target word doesn’t have that letter
• Yellow: the target word has that letter, but in a different position
• Green: the target word has that letter in that exact position

Ideally, you’d use the color of the words to guess the next word you try. For that there are different approaches. I’ll describe the one I follow, where I optimise for removing as many candidates as possible.

#First Word

According to the word list that I use –from this handy Github repo–, there are 12653 English words with exactly 5 letters. Those are our candidates.

There are rumors about target words being always a “common” English word. That’s something we’ll use later, but for our first pick we won’t actually try to guess the target word. We have 0.0079% chances of guessing it right at the first shot. There’s a better way.

As I mentioned in the quick intro, we’ll try to eliminate as many words as possible from our candidates.

#Using the most common letters. Spoiler: wrong.

One thing that I’ve seen do wrong in other approaches, is to build a word with the most common English letters.

There are two things to keep in mind and one problem with this:

1. We shouldn’t take into account letter repetitions in the same word.
2. We should only look at the most common letters in 5 letter words, not all the words.
3. We can do better.

The first point should be clear. We want to discard words, so counting repetitions could wrongly bias us towards picking a letter that appears many times, but not in as many words as other letters.

The second point should be also straight forward. We want to discard words from our candidates, so we should only take those into account.

To illustrate this second point, these are the probabilities of a letter being in a word, in blue for all words, and red for 5 letter words.

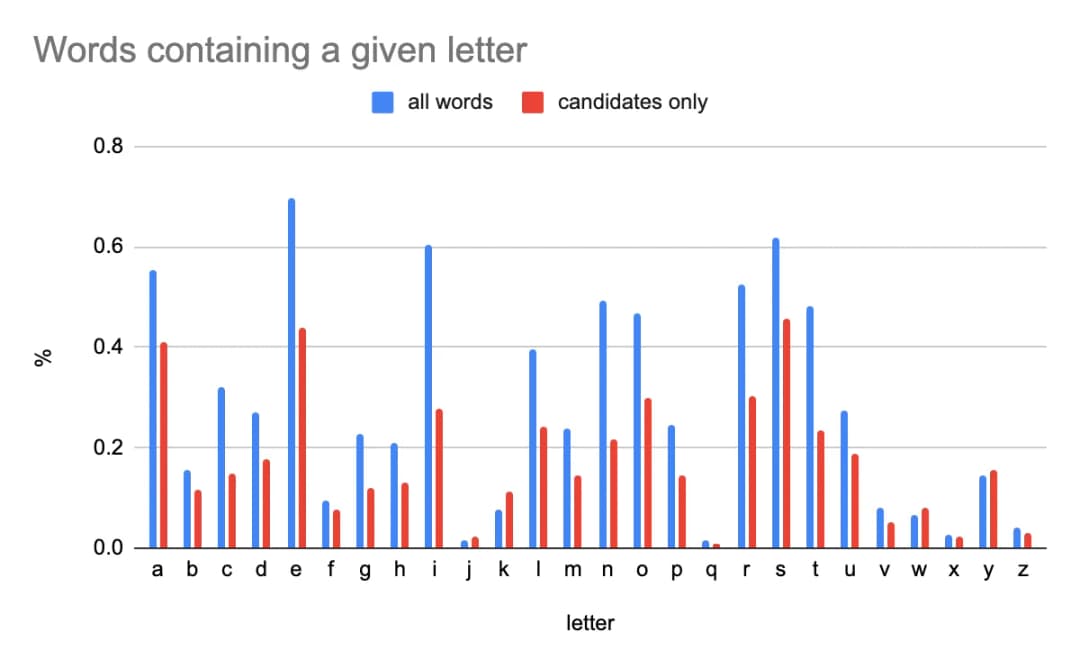
Without getting deeper into the information we get from that chart, let’s just focus on the fact that the % of words having a given letter can be quite different if we only take candidates into account.

Many people I’ve seen sharing their approaches got to this point. But now we reach the 3rd point: we can do better.

#Intersection of words cancelled

I haven’t seen people talking about the intersections between the words cancelled by each letter. Let me try to explain what I mean.

The most common letter in five letter words is S, with 5795 words. The next letter is E, with 5566 words. A is the next with 5205, and so on.

Let’s say we pick a word with the letter S, because that was the most probable, right? But wait a moment. There are 2265 words that have both S and E. That means that out of the 5566 words we could eliminate with the letter E, there are 2265 words already eliminated by the letter S. Do you see where I’m going?

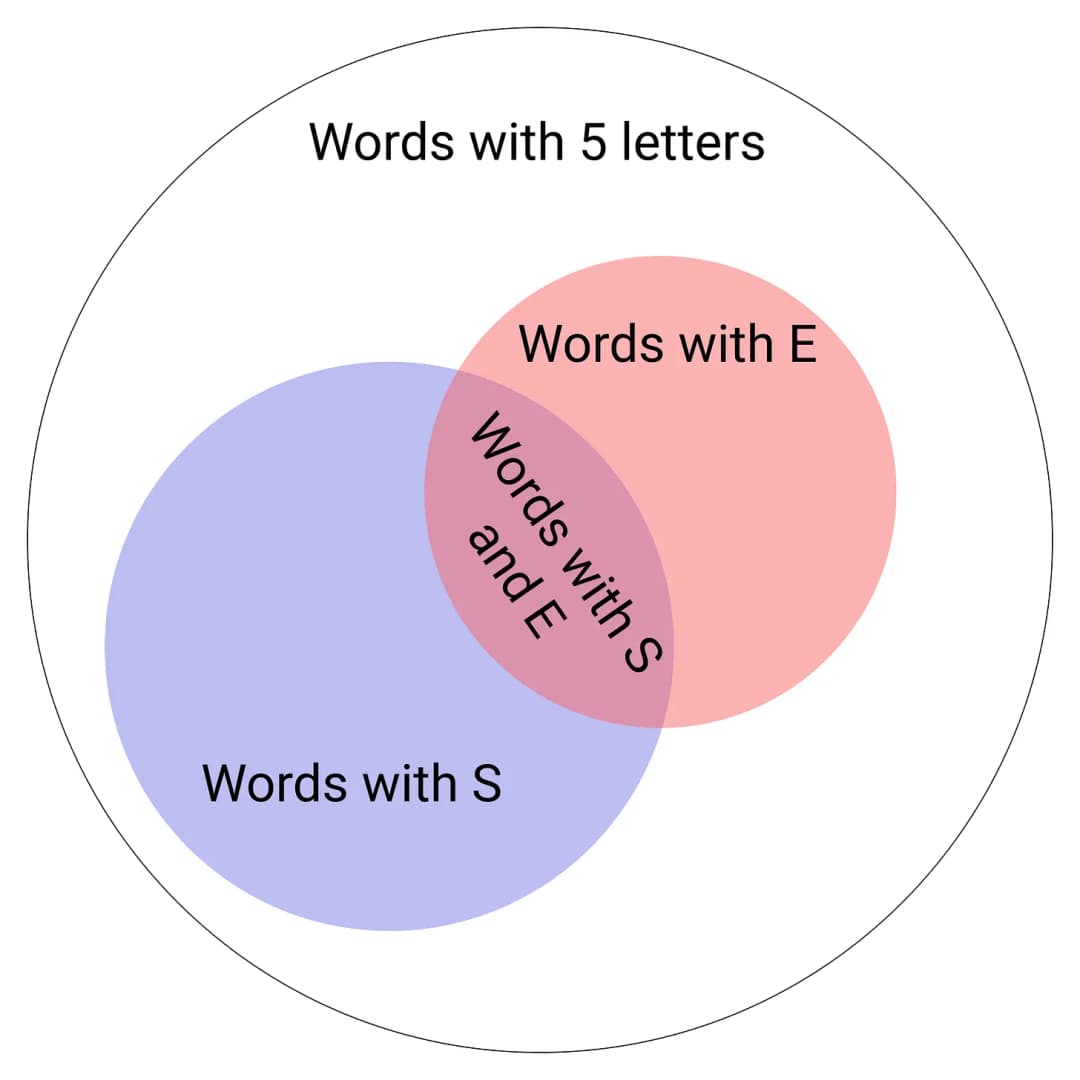
Looking at that image, it looks like we want to increase the area of the union, which means, maximize the amount of words we could eliminate from our candidates.

If you don’t see why this is better, think about this. Picking the most common letters is equivalent to picking the biggest circles possible. If those circles are just on top of each other, you would eliminate the same words just picking one of them, right?

You might want to pick a smaller circle if the combination with the existing ones is the biggest possible. Makes sense?

#The word that cancels more candidates

Alright, but how do we do that?

We could compare every word with each other and count how many a given word would eliminate. There are 12653 words, so we only need 160,098,409 comparisons.

Yes, that’s not great. Feel free to brute force your way or find a clever Dynamic Programming algorithm. The point is, this will give us a list of words sorted by the amount of words cancelled.

In case you’re wondering, this is the list I came up with with this method, with the amount of candidates they eliminate each.

word candidates word candidates

word	candidates	word	candidates
-----	----------	-----	----------
stoae	12115		serai	12043
toeas	12115		paseo	12019
aloes	12109		psoae	12019
aeons	12103		anise	11978
aeros	12088		isnae	11978
arose	12088		saine:	11978
soare	12088		aisle:	11972
aesir	12043		saice:	11950
arise	12043		arsey:	11949
raise	12043		ayres:	11949

What’s a “stoae”? I don’t know –the corrector is actually complaining about it– but the important thing about stoae is that it would remove 95% if none of those letters are in the target word!

Same with “toeas”. No idea what that means –neither does the corrector–, but it takes out the same amount of candidates. Makes sense because they have the same letters.

Nice, so we’ve settled on the first word to try with this method: STOAE.

#Next Rounds

Now we get feedback for the first time. We’ll use that feedback to remove candidates and do the same as we did on the first round, until we have a reasonable amount of them. Somewhere below 20 or 30 should be fine.

Note that every time we remove candidates we need to recalculate the amount of words each candidate would cancel.

Things to keep in mind when incorporating the feedback:

1. If a letter is gray, the letter is not in the target word. That means we remove all the words that have that letter^•.
2. If a letter is green, the letter is in the right position. That means we remove all the words that don’t have that letter in that position.
3. If a letter is yellow, we know two things:
   1. The word has the letter. That means we remove all the words that don’t contain that letter.
   2. The word doesn’t have that letter in that position. That means we remove all the words that have that letter in that position.

I didn’t see 3.b at first, so I’ll put an example to go through all the points.

Say that we’re playing a 4 letter version of the game and we’ve tried LEAN. We don’t know it yet, but the target word is NEXT. We got the feedback: LEAN.

• Because of 1, we filter out all words that contain L or A.
• Because of 2, we filter out all words that don’t have E as 2nd letter.
• Because of 3.a, we filter out all the words that don’t have an N.
• Because of 3.b, we filter out all the words that have an N as the 4th letter. For example, it wouldn’t make sense to try REIN, because we could take advantage of using the N in a different position and get more information. NEST is a definitely better choice.

#Finding the Target

Remember the rumour about the target being always a “common” English word? Now’s when we use this.

For example, take DRINK, the word for January 11th.

The result for each round with this method would have been:

1. Candidate: STOAE. Result: STOAE
2. Candidate: LUPIN. Result: LUPIN.
3. We have 41 candidates. There are still too many common words. We try BRINY. Result BRINY.
4. We have just 4 words remaining in our candidates. These are the words and the amount of candidates they would remove:
   
   GRIND: 4; WRING: 3; IRING: 3; DRINK: 2
   
   If we sorted them by frequency of use, I’d say it would be DRINK, GRIND, WRING, IRING.

At that point we can go either way. If we pick DRINK, we win in 4 rounds. If we pick any other word, the remaining candidate would be DRINK, and we win in 5 rounds.

And that’s a word that gave us the least amount of information possible at the first round, because it didn’t have any letter from our initial candidate. So, I’d say you can expect to complete the game successfully most of the time.

#Possible Improvements

We currently count how many words would be discarded if none of the letters tried are in the target word. That’s the metric we use to sort the candidates as how good they are. It’s like they’re points and we order by the candidate with more points.

But there are infinite ways of giving points to a word. Some improvements can be made here.

#Give points based on frequency

If the rumors are true, it’s clear that discarding a common candidate should give more points than removing a rare word.

#Take positions into the pointing system

I feel we could squeeze more juice out of yellow letters. For example, if we have the following candidates, what would you use?

ABC, ABD, ABE, BAC

The fact that all have the letter B will give them the same points. Any word would eliminate any other word, but we’re not taking advantage of having B in the second position for most of the words.

I’m not sure if there’s much to improve here, but it’s something worth exploring.

#Consider using a word that is not a candidate

What if the word that removes more candidates is not a candidate itself? I guess this is not going to happen too often, but it could definitely happen.

I imagine a situation where a word has been already removed from the candidates, but the combination of letters and their order would give us more information than any other word that’s currently in the candidates list.

It’s possible that this makes no sense at all, but I think it’s worth putting some thoughts on this one.

#The Code

If there’s interest I’ll publish the code on GitHub, but I’d need to do some cleanups and add some comments first. So I won’t invest the time if no one is going to look at it ¯\_(ツ)_/¯